Getting Started with Epinowcast: Nowcasting
Epinowcast Team
Source:vignettes/epinowcast.Rmd
epinowcast.RmdQuick start
In this quick start, we demonstrate using epinowcast to specify and fit a minimal nowcasting model of COVID-19 hospitalisations in Germany. Examples using more complex models are available in other package vignettes and in the papers referenced in the literature vignette.
Package
In this quick start, we also use data.table and ggplot2 packages. These are both installed as dependencies when epinowcast is installed. Note that all output from epinowcast is readily useable with other tools, including tidyverse packages (see here for a comparison).
Code
Data
Nowcasting of right-truncated case counts involves the estimation of reporting delays for recently reported data. For this, we need case counts both by when they were diagnosed (e.g. when someone tests positive; often called “reference date”) and by when they were reported (i.e. when administratively recorded via public health surveillance; often called “report date”). The difference between the reference date and the report date is the reporting delay. For this quick start, we use data from the Robert Koch Institute via the Germany Nowcasting hub. These data represent hospitalisation counts by date of positive test and date of test report in Germany up to October 1, 2021.
Filtering
We first filter to create a snapshot of retrospective data available 40 days before October 1, 2021 that contains 40 days of data. Then, we create the nowcast target which is the latest available hospitalisations by date of positive test. This will allow us to visualise how a nowcast made at the time compares to what was ultimately reported.
Code
nat_germany_hosp <-
germany_covid19_hosp[location == "DE"][age_group == "00+"] |>
enw_filter_report_dates(latest_date = "2021-10-01")
retro_nat_germany <- nat_germany_hosp |>
enw_filter_report_dates(remove_days = 40) |>
enw_filter_reference_dates(include_days = 40)
retro_nat_germany
#> reference_date location age_group confirm report_date
#> <IDat> <fctr> <fctr> <int> <IDat>
#> 1: 2021-07-13 DE 00+ 21 2021-07-13
#> 2: 2021-07-14 DE 00+ 22 2021-07-14
#> 3: 2021-07-15 DE 00+ 28 2021-07-15
#> 4: 2021-07-16 DE 00+ 19 2021-07-16
#> 5: 2021-07-17 DE 00+ 20 2021-07-17
#> ---
#> 857: 2021-07-14 DE 00+ 72 2021-08-21
#> 858: 2021-07-15 DE 00+ 69 2021-08-22
#> 859: 2021-07-13 DE 00+ 59 2021-08-21
#> 860: 2021-07-14 DE 00+ 72 2021-08-22
#> 861: 2021-07-13 DE 00+ 59 2021-08-22This data is already in a format that can be used with epinowcast, as it contains
- a reference date (column
reference_date): the date of the observation, in this example the date of a positive test - a report date (column
report_date): the date of report for a given set of observations by reference date - a count (column
confirm): the total (i.e. cumulative) number of hospitalisations by reference date and report date.
The package also provides a range of tools to convert data from line list, incidence, or other common formats into the required format (see Data converters).
Code
latest_germany_hosp <- nat_germany_hosp |>
enw_latest_data() |>
enw_filter_reference_dates(remove_days = 40, include_days = 40)
head(latest_germany_hosp, n = 10)
#> reference_date location age_group confirm report_date
#> <IDat> <fctr> <fctr> <int> <IDat>
#> 1: 2021-07-13 DE 00+ 60 2021-10-01
#> 2: 2021-07-14 DE 00+ 74 2021-10-01
#> 3: 2021-07-15 DE 00+ 69 2021-10-01
#> 4: 2021-07-16 DE 00+ 49 2021-10-01
#> 5: 2021-07-17 DE 00+ 67 2021-10-01
#> 6: 2021-07-18 DE 00+ 51 2021-10-01
#> 7: 2021-07-19 DE 00+ 36 2021-10-01
#> 8: 2021-07-20 DE 00+ 96 2021-10-01
#> 9: 2021-07-21 DE 00+ 94 2021-10-01
#> 10: 2021-07-22 DE 00+ 99 2021-10-01Preprocessing
Before modelling, the input data needs to be converted into the “reporting triangle” format (see our model description for details). We also need to determine metadata to facilitate the model specification. This includes the number of days of data to use for the reference and report modules, the maximum delay to consider, and, optionally, a grouping (i.e. age group, location, or both) of observations.
We process reported data into the format required for epinowcast and return it in a data.table. At this stage, we need to specify a grouping (i.e age, location) if any.
Code
pobs <- enw_preprocess_data(retro_nat_germany, max_delay = 40)
pobs
#> obs new_confirm latest
#> <list> <list> <list>
#> 1: <data.table[860x9]> <data.table[860x11]> <data.table[41x10]>
#> missing_reference reporting_triangle metareference
#> <list> <list> <list>
#> 1: <data.table[0x6]> <data.table[41x42]> <data.table[41x9]>
#> metareport metadelay time snapshots by groups
#> <list> <list> <int> <int> <list> <int>
#> 1: <data.table[80x12]> <data.table[40x5]> 41 41 1
#> max_delay max_date timestep
#> <num> <IDat> <char>
#> 1: 40 2021-08-22 dayThe returned output is in the form of a data.table with metadata stored as variables. It can be useful to check this output before specifying the model, just to make sure everything is as expected.
Model specification
The epinowcast package is designed to provide users with a flexible and customizable modelling framework. The package comes equipped with several modules that users can utilize to construct models, and also allows users to create their own modules. These ensures that models can be tailored to the user’s specific data and context.
Default nowcasting model
The default nowcasting model in epinowcast consists of three modules:
- A process (expectation) module that models the expected counts by date of reference (
reference_date) - A parametric reference reporting model which models the reporting delay distribution from the date of reference
- A non-parametric reporting model which models differences in the reporting delay distribution by date of report (
report_date), for example, day-of-the-week effects on the reporting delay.
In the following sections, we specify simple models for each of these modules. The appropriateness of these specifications will vary depending on your context. See our vignettes for further details on model specification and examples of more complex models.
Process model
A commonly used process model in nowcasting is to model the expected counts by date of reference via a geometric random walk as this acts as a minimally informed smoothing prior and thus gives a lot of weight to the observed data. This is the default process model in epinowcast. Users may also specify this model for themselves using the enw_expectation() function.
Code
expectation_module <- enw_expectation(
~ 0 + (1 | day), data = pobs
)Here, day refers to the number of days from the start of the data.
As the underlying process model is an exponential growth rate model (\(C_t = C_{t-1} \exp^{r_t}\)), specifying a random effect (i.e. (1 | day)) on the growth rate is equivalent to a geometric random walk on expected counts by reference date.
Reporting model by reference date
Our baseline assumption for the reporting delay is that it is log-normally distributed, and static over time and strata. We can specify this model using the enw_reference() function,
Code
reference_module <- enw_reference(~1, distribution = "lognormal", data = pobs)Note that the default distribution is log-normal, hence the distribution argument could be omitted here. Alternatively we could model the reporting delay non-parametrically using a hazard model (see our model description for details). The following is equivalent to a cox proportional hazards model with a single baseline hazard function.
Code
np_reference_module <- enw_reference(
parametric = ~0, non_parametric = ~ 0 + delay, data = pobs
)Advanced users may wish to combine parametric and non-parametric reference date reporting models. For example, we could model the reporting delay as log-normal for delays up to 10 days and then use a hazard model for longer delays.
Reporting effects by report date
Even where there is evidence that reporting processes can be approximated by a single distribution, there may be additional reporting effects that are not captured by the reference model. For example, reporting may be lower on weekends or holidays. We can specify a model for these effects using a hazard formulation (which captures the conditional relationship between different reporting delays, see our model description for details) using the enw_report() function. Here we specify a model with a random effect for the day of the week to capture weekly seasonality in the reporting delay.
Code
report_module <- enw_report(~ (1 | day_of_week), data = pobs)Precompiling the model
As epinowcast uses cmdstan to fit its models, it is necessary to first compile the model. This can be done using the enw_model() function. Note that this step can be left to epinowcast, but here we want to use multiple cores per chain to speed up model fitting and therefore compile the model with this feature turned on.
Code
model <- enw_model(threads = TRUE)Bringing it all together: Fitting the model
We can now fit the model using the “No-U-Turn Sampler Markov chain Monte Carlo” method. This is a type of Hamiltonian Monte Carlo (HMC) algorithm and is the core fitting method used by cmdstan. The NUTS MCMC method is efficient, automatically tunes its own parameters and is robust to correlations between parameters, making it fast and effective at generating samples from the posterior distribution. We specify fitting options using enw_fit_opts() (note that the settings shown here are tuned for speed and may not be appropriate for many real world use cases). We also pass our preprocessed data (pobs), our pre-compiled model (model), and our model modules (expectation_module, reference_module, and report_module) to epinowcast, where they are combined and used to fit the model.
Code
options(mc.cores = 2)
nowcast <- epinowcast(data = pobs,
expectation = expectation_module,
reference = reference_module,
report = report_module,
fit = enw_fit_opts(
save_warmup = FALSE, pp = TRUE,
chains = 2, threads_per_chain = 2,
iter_sampling = 500, iter_warmup = 500,
show_messages = FALSE
),
model = model
)The epinowcast object
The epinowcast() function returns an epinowcast object which includes diagnostic information, the data used for fitting, and the underlying CmdStanModel object.
Code
nowcast
#> obs new_confirm latest
#> <list> <list> <list>
#> 1: <data.table[860x9]> <data.table[860x11]> <data.table[41x10]>
#> missing_reference reporting_triangle metareference
#> <list> <list> <list>
#> 1: <data.table[0x6]> <data.table[41x42]> <data.table[41x9]>
#> metareport metadelay time snapshots by groups
#> <list> <list> <int> <int> <list> <int>
#> 1: <data.table[80x12]> <data.table[40x5]> 41 41 1
#> max_delay max_date timestep priors
#> <num> <IDat> <char> <list>
#> 1: 40 2021-08-22 day <data.table[14x6]>
#> fit
#> <list>
#> 1: <CmdStanMCMC>\n Inherits from: <CmdStanFit>\n Public:\n clone: function (deep = FALSE) \n cmdstan_diagnose: function () \n cmdstan_summary: function (flags = NULL) \n code: function () \n constrain_variables: function (unconstrained_variables, transformed_parameters = TRUE, \n data_file: function () \n diagnostic_summary: function (diagnostics = c("divergences", "treedepth", "ebfmi"), \n draws: function (variables = NULL, inc_warmup = FALSE, format = getOption("cmdstanr_draws_format", \n expose_functions: function (global = FALSE, verbose = FALSE) \n functions: environment\n grad_log_prob: function (unconstrained_variables, jacobian = TRUE, jacobian_adjustment = NULL) \n hessian: function (unconstrained_variables, jacobian = TRUE, jacobian_adjustment = NULL) \n init: function () \n init_model_methods: function (seed = 0, verbose = FALSE, hessian = FALSE) \n initialize: function (runset) \n inv_metric: function (matrix = TRUE) \n latent_dynamics_files: function (include_failed = FALSE) \n log_prob: function (unconstrained_variables, jacobian = TRUE, jacobian_adjustment = NULL) \n loo: function (variables = "log_lik", r_eff = TRUE, moment_match = FALSE, \n lp: function () \n metadata: function () \n num_chains: function () \n num_procs: function () \n output: function (id = NULL) \n output_files: function (include_failed = FALSE) \n print: function (variables = NULL, ..., digits = 2, max_rows = getOption("cmdstanr_max_rows", \n profile_files: function (include_failed = FALSE) \n profiles: function () \n return_codes: function () \n runset: CmdStanRun, R6\n sampler_diagnostics: function (inc_warmup = FALSE, format = getOption("cmdstanr_draws_format", \n save_data_file: function (dir = ".", basename = NULL, timestamp = TRUE, random = TRUE) \n save_latent_dynamics_files: function (dir = ".", basename = NULL, timestamp = TRUE, random = TRUE) \n save_object: function (file, ...) \n save_output_files: function (dir = ".", basename = NULL, timestamp = TRUE, random = TRUE) \n save_profile_files: function (dir = ".", basename = NULL, timestamp = TRUE, random = TRUE) \n summary: function (variables = NULL, ...) \n time: function () \n unconstrain_draws: function (files = NULL, draws = NULL, format = getOption("cmdstanr_draws_format", \n unconstrain_variables: function (variables) \n variable_skeleton: function (transformed_parameters = TRUE, generated_quantities = TRUE) \n Private:\n draws_: -1475.14 -1481.86 -1476.55 -1486.67 -1478.49 -1482.47 -1 ...\n init_: NULL\n inv_metric_: list\n metadata_: list\n model_methods_env_: environment\n profiles_: NULL\n read_csv_: function (variables = NULL, sampler_diagnostics = NULL, format = getOption("cmdstanr_draws_format", \n return_codes_: 0 0\n sampler_diagnostics_: 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 ...\n warmup_draws_: NULL\n warmup_sampler_diagnostics_: NULL
#> data fit_args samples max_rhat divergent_transitions
#> <list> <list> <int> <num> <num>
#> 1: <list[116]> <list[7]> 1000 1.02 0
#> per_divergent_transitions max_treedepth no_at_max_treedepth
#> <num> <num> <int>
#> 1: 0 8 4
#> per_at_max_treedepth run_time
#> <num> <num>
#> 1: 0.004 41.9Summarising and plotting the nowcast
The nowcast (the combination of currently observed and predicted unobserved data) can then be summarised using
Code
nowcast |>
summary(probs = c(0.05, 0.95)) |>
head(n = 10)
#> reference_date report_date .group max_confirm location age_group
#> <IDat> <IDat> <num> <int> <fctr> <fctr>
#> 1: 2021-07-14 2021-08-22 1 72 DE 00+
#> 2: 2021-07-15 2021-08-22 1 69 DE 00+
#> 3: 2021-07-16 2021-08-22 1 47 DE 00+
#> 4: 2021-07-17 2021-08-22 1 65 DE 00+
#> 5: 2021-07-18 2021-08-22 1 50 DE 00+
#> 6: 2021-07-19 2021-08-22 1 36 DE 00+
#> 7: 2021-07-20 2021-08-22 1 94 DE 00+
#> 8: 2021-07-21 2021-08-22 1 91 DE 00+
#> 9: 2021-07-22 2021-08-22 1 99 DE 00+
#> 10: 2021-07-23 2021-08-22 1 86 DE 00+
#> confirm cum_prop_reported delay prop_reported mean median sd
#> <int> <num> <num> <num> <num> <num> <num>
#> 1: 72 1 39 0 72.000 72 0.0000000
#> 2: 69 1 38 0 69.039 69 0.2180058
#> 3: 47 1 37 0 47.090 47 0.2966277
#> 4: 65 1 36 0 65.241 65 0.5011688
#> 5: 50 1 35 0 50.288 50 0.5507807
#> 6: 36 1 34 0 36.278 36 0.5504716
#> 7: 94 1 33 0 94.517 94 0.7498488
#> 8: 91 1 32 0 91.794 92 0.9297464
#> 9: 99 1 31 0 100.142 100 1.1203085
#> 10: 86 1 30 0 87.383 87 1.2449341
#> mad q5 q95 rhat ess_bulk ess_tail
#> <num> <num> <num> <num> <num> <num>
#> 1: 0.0000 72 72 NA NA NA
#> 2: 0.0000 69 69 1.0006406 1074.7070 1061.6479
#> 3: 0.0000 47 48 1.0001351 1037.1523 1013.5831
#> 4: 0.0000 65 66 1.0016224 1002.5895 972.2167
#> 5: 0.0000 50 51 0.9998357 948.7085 955.4453
#> 6: 0.0000 36 37 1.0017104 866.5944 880.2667
#> 7: 0.0000 94 96 1.0003799 986.0193 835.5012
#> 8: 1.4826 91 94 0.9990671 1182.9177 1028.3864
#> 9: 1.4826 99 102 1.0004965 1012.8400 1025.7233
#> 10: 1.4826 86 90 1.0004209 1015.0868 861.2164Similarly, the summarised nowcast can be plotted against the latest observed data using
Code
plot(nowcast, latest_obs = latest_germany_hosp)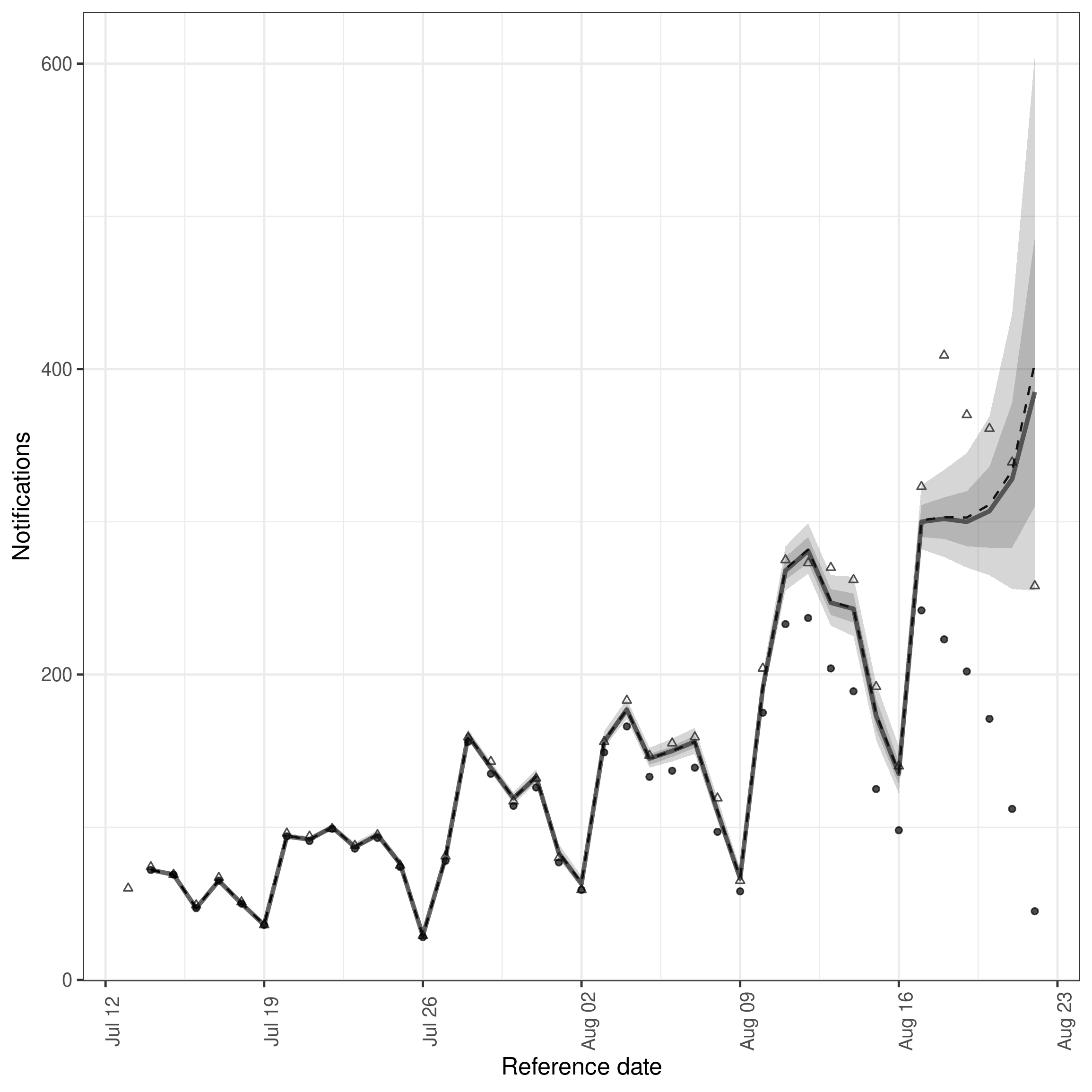
plot of chunk nowcast
Plotting posterior predictions
Plotting posterior predictions can be a useful way of assessing performance and checking that the model is capturing the underlying data generation process adequately. We can do this directly on the output of epinowcast() using
Code
plot(nowcast, type = "posterior") +
facet_wrap(vars(reference_date), scale = "free")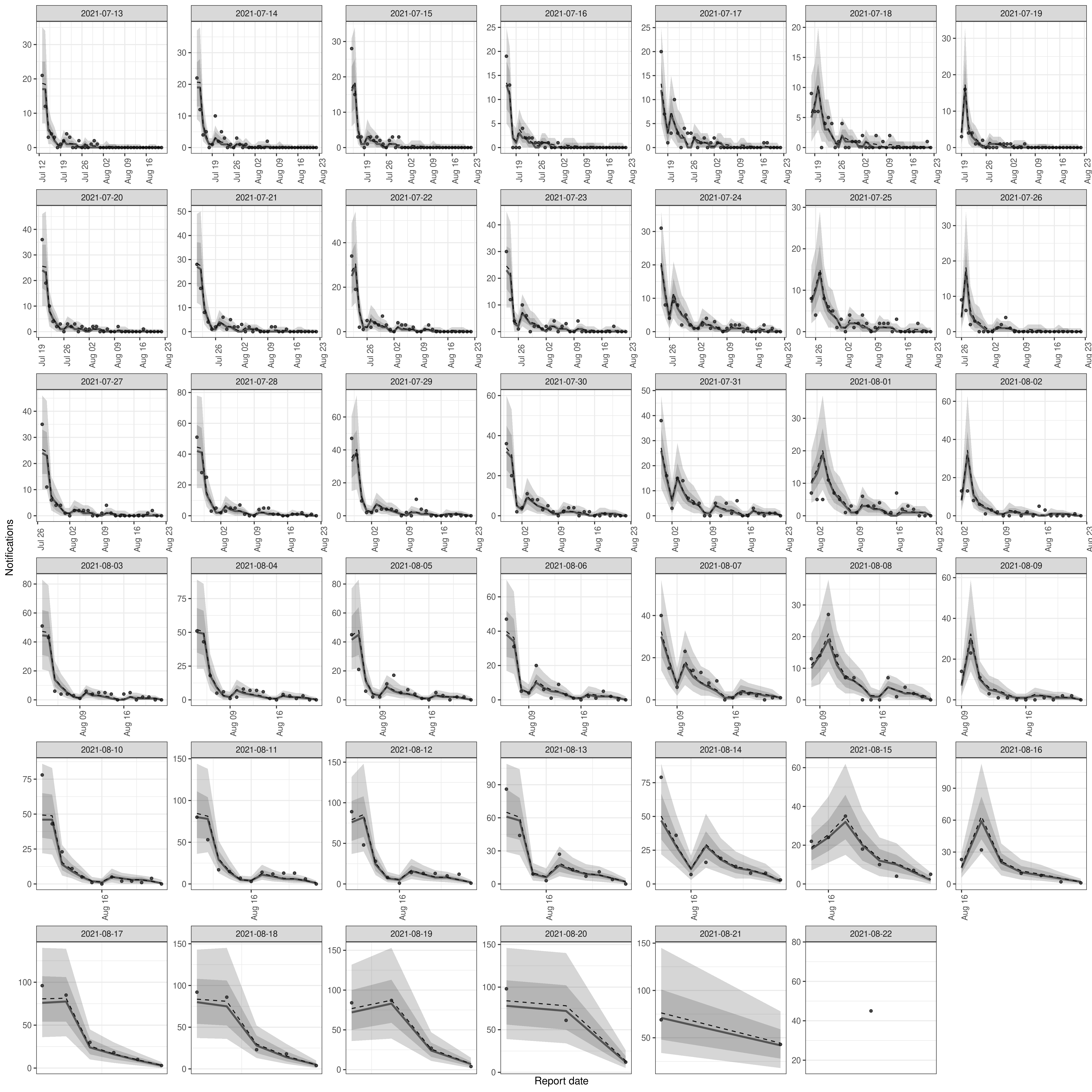
plot of chunk pp
Using package functions rather than S3 methods
Rather than using S3 methods supplied for epinowcast() directly, package functions can also be used to extract nowcast posterior samples, summarise them, and then plot them. This is demonstrated here by plotting the 7 day incidence for hospitalisations.
Code
# extract samples
samples <- summary(nowcast, type = "nowcast_samples")
# Take a 7 day rolling sum of both samples and observations
cols <- c("confirm", "sample")
samples[, (cols) := lapply(.SD, frollsum, n = 7),
.SDcols = cols, by = ".draw"
][!is.na(sample)]
#> reference_date report_date .group max_confirm location age_group
#> <IDat> <IDat> <num> <int> <fctr> <fctr>
#> 1: 2021-07-20 2021-08-22 1 94 DE 00+
#> 2: 2021-07-20 2021-08-22 1 94 DE 00+
#> 3: 2021-07-20 2021-08-22 1 94 DE 00+
#> 4: 2021-07-20 2021-08-22 1 94 DE 00+
#> 5: 2021-07-20 2021-08-22 1 94 DE 00+
#> ---
#> 33996: 2021-08-22 2021-08-22 1 45 DE 00+
#> 33997: 2021-08-22 2021-08-22 1 45 DE 00+
#> 33998: 2021-08-22 2021-08-22 1 45 DE 00+
#> 33999: 2021-08-22 2021-08-22 1 45 DE 00+
#> 34000: 2021-08-22 2021-08-22 1 45 DE 00+
#> confirm cum_prop_reported delay prop_reported .chain .iteration
#> <int> <num> <num> <num> <int> <int>
#> 1: 433 1 33 0 1 1
#> 2: 433 1 33 0 1 2
#> 3: 433 1 33 0 1 3
#> 4: 433 1 33 0 1 4
#> 5: 433 1 33 0 1 5
#> ---
#> 33996: 1093 1 0 1 2 496
#> 33997: 1093 1 0 1 2 497
#> 33998: 1093 1 0 1 2 498
#> 33999: 1093 1 0 1 2 499
#> 34000: 1093 1 0 1 2 500
#> .draw sample
#> <int> <num>
#> 1: 1 438
#> 2: 2 433
#> 3: 3 433
#> 4: 4 434
#> 5: 5 433
#> ---
#> 33996: 996 2083
#> 33997: 997 2394
#> 33998: 998 2335
#> 33999: 999 2421
#> 34000: 1000 2203
latest_germany_hosp_7day <- copy(latest_germany_hosp)[
,
confirm := frollsum(confirm, n = 7)
][!is.na(confirm)]
# Summarise samples
sum_across_last_7_days <- enw_summarise_samples(samples)
# Plot samples
enw_plot_nowcast_quantiles(sum_across_last_7_days, latest_germany_hosp_7day)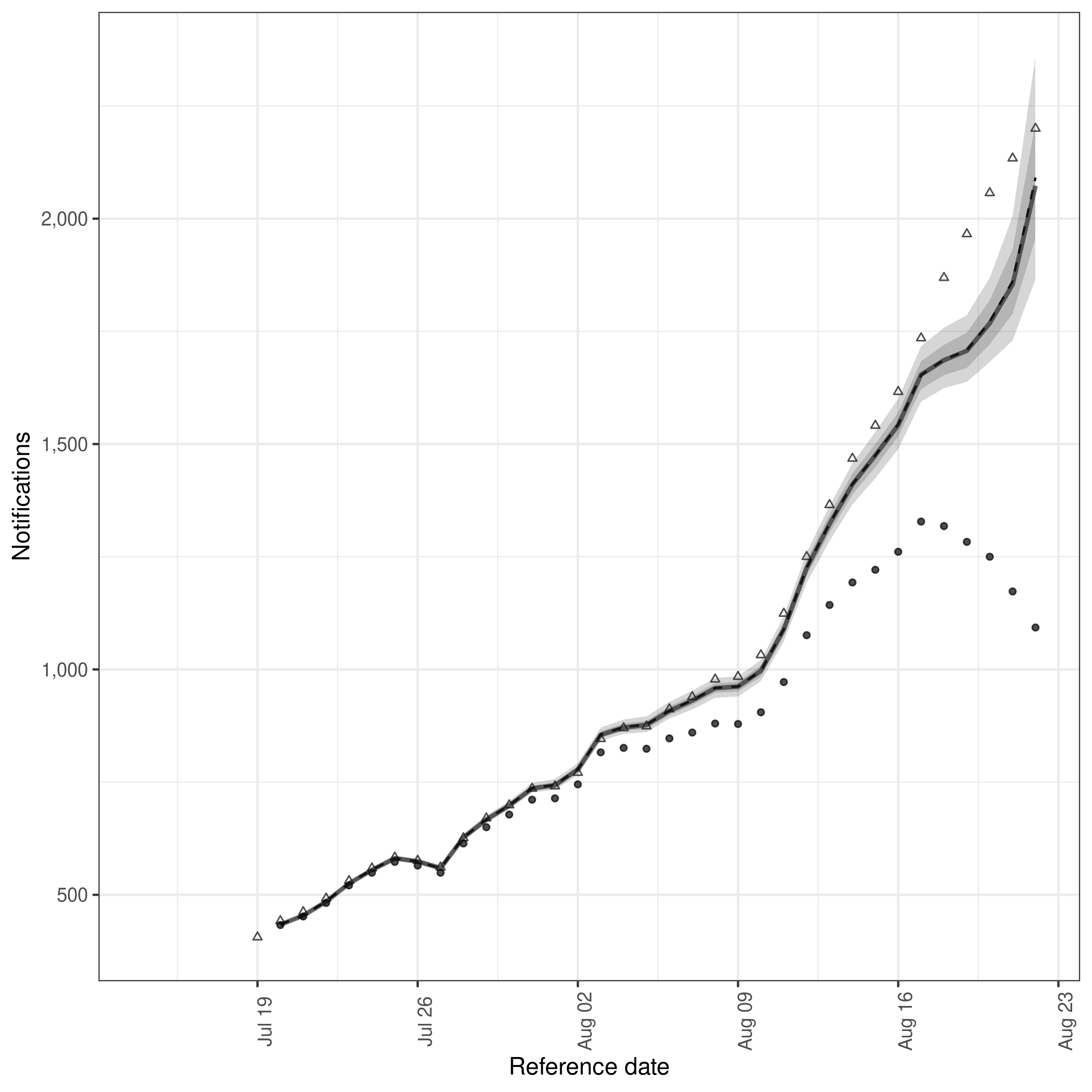
plot of chunk week_nowcast
Here we see that the model is underestimating the incidence of hospitalisations that were ultimately reported. There are a range of potential reasons for this, the first being that the process model does not fully capture the trend or day of the week periodicity present in the data. See our case study vignettes for ideas on how deal with such issues.